Для начала немного жути :)
По определению Коши предел функции в точке x0 есть действительнозначное число А, если для любого
достаточно малого числа e>0 найдется число d(e) *зависящий от е* такое, что в любой точке
окрестности x0 |x-xo|<d(e) выполняется условие |f(x)-A|<e
Другими словами, предел есть значение, к которому функция стремится при стремлении аргумента к некоторой точке, которую называют предельной, причем аргумент можно устремить и в бесконечность, и в нуль (оба эти предельные значения чаще всего и используются). Это фундаментальное понятие, на котором строится далее весь матанализ. Людям, в силу субъективных обстоятельств, ненавидевших математику в школе, наверно, понятнее будет наглядно ниже.
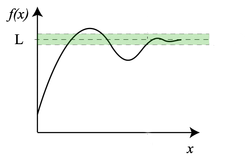
Функция f(x) стремится к L при x стремящемся к бесконечности.
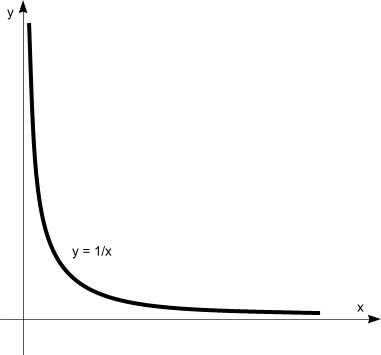
Функция f(x)=1\x при x стремящемся к нулю, стремится к бесконечности, и наоборот, при x стремящемся к бесконечности, сама стремится к нулю. Очевидность, думаю, более чем ясная.
Вспоминая школьный курс алгебры и начал анализа, у меня возникает чувство, что в понятии предела, помимо сугубо математического смысла, заложено представление об Истине, как о чем-то абсолютном и тривиальном.
Далее - почти бредовое...
Есть истины очевидные - существуют функции, которые одновременно являются пределами для самих же себя.
Есть истины безграничные как космос - для линейной возрастающей функции предел есть бесконечность.
А есть истины, которые где-то рядом *их искали агенты Малдер и Скалли :D*, но которые никогда не будут доступны для нашего понимания. Ровно так же, как две вышеописанные функции стремятся к своим пределам, мы на протяжении времени становимся к этим истинам ближе и ближе, но это всего лишь иллюзия доступности. За очередной преодоленной стеной вырастает следующая, менее толстая, но уже более высокая... Люди, устав преодолевать эти препятствия, оградились от Истины религией, искусством, да даже просто похуизмом.
В реальности же, у меня такое ощущение что очевидных истин первого рода не существует. Равно как и такие функции не могут описывать объективно процессы в нашей жизни. Остается или локально стремиться к Истине-идеалу, или плыть в бездну знаний, где Истина есть бесконечность.
Вы думаете, площадь стола равна 1,25 квадратных метров? Черта-с два, если копнуть глубже, рациональные числа всего лишь ограничивают наше видение мира от лишней головной боли. Представьте, даже самый гладкий отшлифованный стол не будет идеально ровным - на нем миллиарды миллиардов косых хребтов и сколов, сумма площадей которых будет намного больше чем просто число, полученное в результате умножения длины стола на его ширину; мне трудно представить, насколько больше настоящая площадь стола относительно той, что мы берем за Истину.
А она, к сожалению, или, к счастью, недостижима.
|Все еще хочешь узнать, кто круче - Сталлоне или Шварцнеггер? :)
