Хочу рассказать об одном интересном и полезном, с моей точки зрения, для общего развития применении таких базовых структур данных, как стек и очередь, на которые, к сожалению, неоправданно забивают многие будущие программисты при обучении. Первый раз оно было встречено на зимних сборах 2008 года в Петрозаводске (огромное спасибо Андрею Станкевичу за разбор), а вскоре к нему неожиданно свелась задача для Республиканской олимпиады школьников (правда, там для облегчения проходило и не самое оптимальное решение, но это, увы, не сильно помогло участникам).
Примерная суть задачи:
Дан массив A из N целых чисел (N порядка 108) и целое K (K < 106). Необходимо для каждого i от 1 до N - K + 1 найти min(A[i], A[i + 1], … A[i + K - 1]). Иначе говоря, в каждых K последовательных элементах массива найти минимальный. Время работы 2-3 секунды.
Лобовое решение имеет временную оценку примерно O(NK). Более умное, с использованием дерева отрезков, сбалансированных двоичных деревьев или чего-то подобного — O(NlogK). Но, к сожалению, это не достаточно быстро — необходима строго линейная зависимость времени работы от размера входных данных.
Для начала слегка преобразуем задачу. Пойдем по данному массиву слева направо и будем добавлять его элементы в очередь. При этом, если в размер очереди становится ровно K + 1, будем сразу выбрасывать из нее один элемент. Теперь задача в следующем: в каждый момент нам нужно уметь за константное (O(1)) время находить минимум в очереди. Как это сделать?
Сначала научимся делать то же самое в стеке. Для этого, параллельно со стеком S1, где хранятся сами элементы, заведем еще один — S2. При помещении числа X в первый стек, во второй будем помещать min(X, top(S2)), где top(S2) — элемент, находящийся на вершине стека S2. Тогда в каждый момент времени i-й элемент (считая снизу) в стеке S2 будет минимумом из нижних i элементов стека S1, а, следовательно элемент на вершине стека S2 будет минимумом из всех элементов стека S1. Очевидно, что это свойство также будет сохраняться при одновременном выталкивании элементов из стеков. Так как получение верхнего элемента стека осуществляется за константное время, то для стека задача решена.
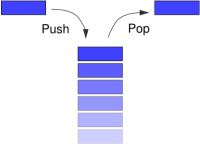
Теперь попробуем применить полученный результат к нашей задаче. Идея указана в заголовке статьи — смоделируем очередь двумя стеками T1 и T2. Класть новые элементы будем только в T1. Забирать — только из T2. При этом, если в стеке T2 пусто, то нужно перенести в него все элементы из T1. Очевидно, что над каждым элементом выполняется максимум 3 константные операции, и, как следствие, получаем амортизированную линейную зависимость времени работы от количества операций.
Далее — дело техники: найти минимум в каждом из стеков мы уже можем, а минимум в очереди будет min(min(T1), min(T2)), где min(T1), min(T2) — минимум в стеке T1 или T2 соответственно.
Кросспост с моего блога.